Machine learning derivatives

Published on 06/03/2021

Derivatives are frequently used in machine learning because it allows us to efficiently train a neural network. An analogy would be finding which direction you should take to reach the highest mountain but with the restriction of only being able to see one meter away. In this article, we will first recall the rules of derivatives and partial derivatives. Then we will feature a few derivatives of functions that are commonly used in machine learning.

The derivatives rules

The basics

Let’s start by the derivatives of common functions. In the following :

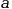is a constant
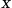is the variable by which we derive the functions
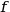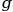and are functions
Also note that 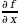is equivalent to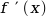

Function

Derivative

Here are a few derivative rules that we will use in the following sections.

Rule

Function

Derivative

Multiplication by a constant

Sum

Difference

Product

Quotient

Reciprocal (from quotient)

The chain rule

$(f \circ g)' = (f' \circ g) \cdot g'$

means . We can also rewrite it using Leibniz’s notation :

$\frac{\partial f}{\partial x} = \frac{\partial f}{\partial g} \cdot \frac{\partial g}{\partial x}$

Which literally says : the derivative by is the derivative by () multiplied by the derivative .

Partial derivatives and gradient

Let’s define a function :

How can we calculate the derivative of this function ?

When a functions takes more than one variable as an argument, we can calculate the derivative of the function with respect to each variable. When we do that, the variables are treated as constants :

$\frac{\partial f}{\partial x} = \frac{\partial (x^2 - 3 \cdot a)}{\partial x} = 2x - 0 = 2x$

$\frac{\partial f}{\partial y} = \frac{\partial (a^2 - 3 y)}{\partial x} = 0 - 3 = -3$

We define the gradient of a function as the vector of all its parial derivatives, in this case the gradient of the function is :

$\nabla f = (2x, -3)$

More generally, for a function that takes a vector as an argument, its gradient is defined by .

The sigmoid

A sigmoid is a "S"-shaped curve. The one we use is called the logistic function and it is defined like this :

$sigmoid(x) = f(x) = \frac{1}{1 + e^{-x}}$

Here is a graph of what it looks like, along with its derivative :

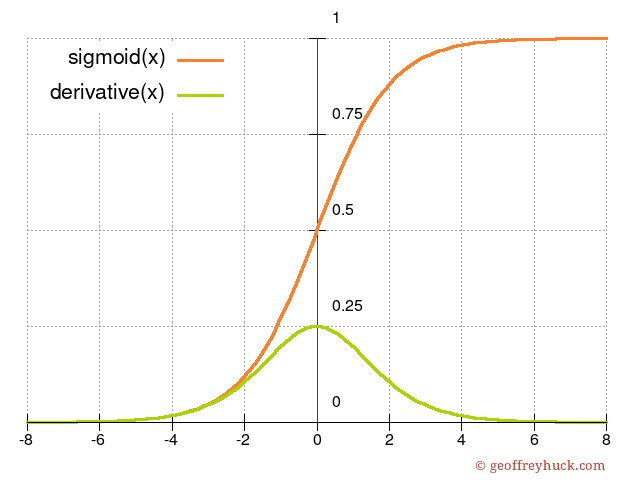
Figure 1. The sigmoid function and its derivative

Let’s compute its derivative :

$f(x) = \frac{1}{1 + e^{-x}}$

$f'(x) = -\frac{1}{(1 + e^{-x})^2} \cdot \frac{\partial (1 + e^{-x})}{\partial x}$

After using the reciprocal rule. Now we first calculate the right part using again the reciprocal rule :

$\frac{\partial (1 + e^{-x})}{\partial x} = \frac{\partial (\frac{1}{e^{x}})}{\partial x} = -\frac{e^x}{(e^x)^2} = -\frac{1}{e^x} = -e^{-x}$

So we have :

$f'(x) = -\frac{1}{(1 + e^{-x})^2} \cdot (-e^{-x}) = \frac{1}{(1 + e^{-x})^2} \cdot e^{-x} = \frac{1}{1 + e^{-x}} \cdot \frac{e^{-x}}{1 + e^{-x}}$

Now we use a little trick on the right part, adding on the top :

$f'(x) = \frac{1}{1 + e^{-x}} \cdot \left(\frac{1 + e^{-x} - 1}{1 + e^{-x}}\right) = \frac{1}{1 + e^{-x}} \cdot \left(\frac{1 + e^{-x}}{1 + e^{-x}} - \frac{1}{1 + e^{-x}}\right) = \frac{1}{1 + e^{-x}} \cdot \left(1 - \frac{1}{1 + e^{-x}}\right)$

You remember that ? So we can write :

$f' = f \cdot (1 - f)$

$\frac{\partial (sigmoid)}{\partial x} = sigmoid(x) \cdot (1 - sigmoid(x))$

The squared error function

The squared error function is defined by :

$squared\_error(predicted\_output) = \frac{1}{2} \cdot (true\_output - predicted\_output)^2$

We usually use this function for a batch of examples, which gives us the following formula where the variables are vectors :

$squared\_error(\mathbf{predicted\_output}) = \frac{1}{2} \cdot \sum_{i=1}^{n\_examples} (\mathbf{true\_output}_{[i]} - \mathbf{predicted\_output}_{[i]})^2$

And sometimes, the output of an example is itself a vector (think about an artificial neural network with multiple output units), we then have the following where the variables are matrices :

$squared\_error(Predicted\_output) = \frac{1}{2} \cdot \sum_{i=1}^{n\_examples} \sum_{j=1}^{n\_outputs} (True\_output_{[i][j]} - Predicted\_output_{[i][j]})^2$

The square of a difference is always positive, therefore the more difference there is between the true output and the predicted output, the bigger the result. The term is only used because it makes the derivative more convenient, as you we see.

Now what we want is the partial derivative with respect to :

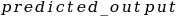for the first variant of the function;
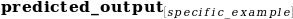for the second variant;
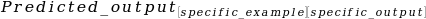for the third variant.

When we calculate a partial derivative, all the other variables are treated as a constant. This means that in the case of the third variant, each that are not of indexes will have a derivative equal to .

Therefore we can get rid of the sums for the calculations of the partial derivatives of , which means we only have to consider the first variant.

We will name the specific variable we derive the function for , and the corresponding true output .

Now let’s start :

$f(x) = \frac{1}{2} \cdot (a - x)^2$

$f'(x) = \frac{1}{2} \cdot 2 \cdot (a - x) \cdot (-1)$

After using the chain rule. Now let’s simplify the result :

$\frac{\partial (squared\_error)}{\partial predicted\_output} = predicted\_output - true\_output$

Or for the second variant :

$\frac{\partial (squared\_error)}{\partial \mathbf{predicted\_output}_{[specific\_example]}} = \mathbf{predicted\_output}_{[specific\_example]} - \mathbf{true\_output}_{[specific\_example]}$

And for the third variant :

$\frac{\partial (squared\_error)}{\partial Predicted\_output_{[specific\_example][specific\_output]}} =$

$Predicted\_output_{[specific\_example][specific\_output]} - True\_output_{[specific\_example][specific\_output]}$